ADATA XPG V2 Review: 2x8 GB at DDR3-2800 12-14-14 1.65 V
by Ian Cutress on December 17, 2013 12:00 PM ESTCPU Compute
One side I like to exploit on CPUs is the ability to compute and whether a variety of mathematical loads can stress the system in a way that real-world usage might not. For these benchmarks we are ones developed for testing MP servers and workstation systems back in early 2013, such as grid solvers and Brownian motion code. Please head over to the first of such reviews where the mathematics and small snippets of code are available.
3D Movement Algorithm Test
The algorithms in 3DPM employ uniform random number generation or normal distribution random number generation, and vary in various amounts of trigonometric operations, conditional statements, generation and rejection, fused operations, etc. The benchmark runs through six algorithms for a specified number of particles and steps, and calculates the speed of each algorithm, then sums them all for a final score. This is an example of a real world situation that a computational scientist may find themselves in, rather than a pure synthetic benchmark. The benchmark is also parallel between particles simulated, and we test the single thread performance as well as the multi-threaded performance. Results are expressed in millions of particles moved per second, and a higher number is better.
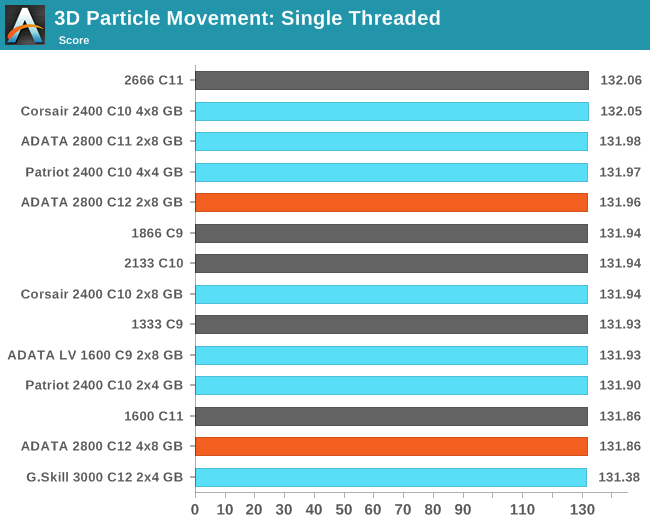
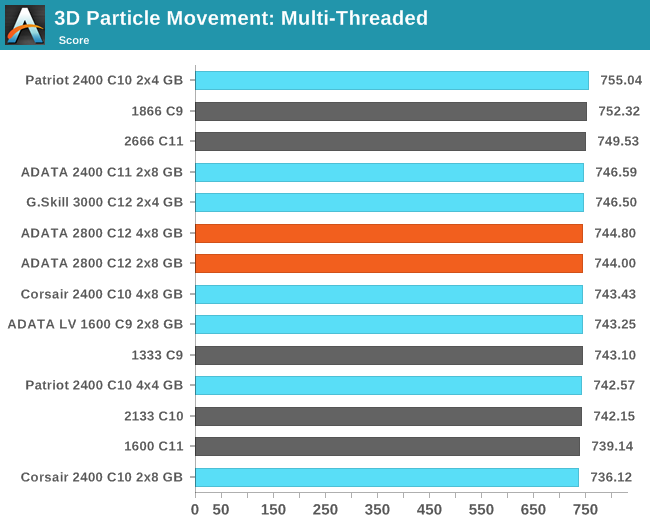
N-Body Simulation
When a series of heavy mass elements are in space, they interact with each other through the force of gravity. Thus when a star cluster forms, the interaction of every large mass with every other large mass defines the speed at which these elements approach each other. When dealing with millions and billions of stars on such a large scale, the movement of each of these stars can be simulated through the physical theorems that describe the interactions. The benchmark detects whether the processor is SSE2 or SSE4 capable, and implements the relative code. We run a simulation of 10240 particles of equal mass - the output for this code is in terms of GFLOPs, and the result recorded was the peak GFLOPs value.

Grid Solvers - Explicit Finite Difference
For any grid of regular nodes, the simplest way to calculate the next time step is to use the values of those around it. This makes for easy mathematics and parallel simulation, as each node calculated is only dependent on the previous time step, not the nodes around it on the current calculated time step. By choosing a regular grid, we reduce the levels of memory access required for irregular grids. We test both 2D and 3D explicit finite difference simulations with 2n nodes in each dimension, using OpenMP as the threading operator in single precision. The grid is isotropic and the boundary conditions are sinks. We iterate through a series of grid sizes, and results are shown in terms of ‘million nodes per second’ where the peak value is given in the results – higher is better.


Grid Solvers - Implicit Finite Difference + Alternating Direction Implicit Method
The implicit method takes a different approach to the explicit method – instead of considering one unknown in the new time step to be calculated from known elements in the previous time step, we consider that an old point can influence several new points by way of simultaneous equations. This adds to the complexity of the simulation – the grid of nodes is solved as a series of rows and columns rather than points, reducing the parallel nature of the simulation by a dimension and drastically increasing the memory requirements of each thread. The upside, as noted above, is the less stringent stability rules related to time steps and grid spacing. For this we simulate a 2D grid of 2n nodes in each dimension, using OpenMP in single precision. Again our grid is isotropic with the boundaries acting as sinks. We iterate through a series of grid sizes, and results are shown in terms of ‘million nodes per second’ where the peak value is given in the results – higher is better.











19 Comments
View All Comments
YuLeven - Tuesday, December 17, 2013 - link
Thanks for the review.But with all due respect to this site that makes one of the best hardware coverage in English, I'm kind missing interesting stories lately. The late 2013 MacBook Pro, some Windows tablets, GPUs, CPUs, operate systems... anything.
As fat as real world performance is concerned, RAM impact is so negligible for the vast majority of users that this sort of article ends kinda of... boring.
Yet again, thank you for the article. I meant no offence in any way!
SeeManRun - Tuesday, December 17, 2013 - link
Definitely agree with this one...Zak - Tuesday, December 17, 2013 - link
I have to agree that these memory articles are uninteresting and not particularly useful. As others pointed out -- and these articles confirm -- the real life difference between decent DDR1600 and super-duper ultra-high-end RAM are virtually non-existent. One article summarizing that would be more than enough.jeffrey - Tuesday, December 17, 2013 - link
Ian Cutress,Hello again! This is another article stating 1866/C9 being the minimum for Haswell and to avoid 1600 or less. Even going so far as to say, "Any kit 1600 MHz or less is usually bad news."
However, this ignores 1600/C8 modules. The 1600/C8 score a 200 on your Performance Index at stock timings. This is at your recommended 200 level. There are several kits of 2x4 GB 1600/C8 on Newegg that have memory profiles of 8-8-8-24 at 1.5v. I'll repeat, these 1600 8-8-8-24 1.5v kits score 200 on the Performance Index and hit the current memory sweet spot for most people of 2x4 GB. This scores very close to the 1866/C9 kits which have a Performance Index score of 207.
The reason I bring this up is that the 1600 8-8-8-24 kits are often less expensive than the 1866/C9 kits and offer essentially all of the performance.
I enjoy reading your articles and appreciate how active you have been lately!
The_Assimilator - Tuesday, December 17, 2013 - link
This is why I am sticking with my DDR3-1600/CL7 memory until DDR4 hits mainstream. PI = 228 which is faster than 1866/CL9.jeffrey - Tuesday, December 17, 2013 - link
Ian, any comment on 1600/C7 or 1600/C8?Gigaplex - Tuesday, December 17, 2013 - link
"In this graph the x-axis is the Performance Index of the DRAM, and thus a PI of 200 can be 1600 C8 or 2400 C12."This article does not ignore 1600/C8 modules.
Popskalius - Sunday, February 23, 2014 - link
hi, i'm new to ddr3 lol. Re: haswell & 1600/C8, anandtech's intel gaming rig pairs an i5 with 1600/C9. Is this bc it's the cheapest build so not worth the price/performance, or is there really something bad about mixing haswell with anything slower than 1600/c8?thanks a bunch
Senti - Tuesday, December 17, 2013 - link
And another incompetent article from Ian... Didn't even bother to read comments to the previous one to correct errors...Oh, and my IP (range?) is still blacklisted by stupid spam filter. Of course, I probably not love my job enough...
AncientWisdom - Tuesday, December 17, 2013 - link
Lol maybe it should spam filter depending on the job happiness scale, seems legit.